
| Copyright 1995, 1999 by Donald R. Tveter |
| http://www.dontveter.com drt@christianliving.net, don@dontveter.com |
| Commercial Use Prohibited |
In this section we will look at some of the extra features that PROLOG has that PROLOG programmers will find necessary and useful.
The first of the practical features of PROLOG to look at are the consult and listing ``predicates". Consult and listing (and many other predicates) are effectively commands to do something. The consult command lets users read facts and rules off of a file and into the interpreter. A typical command would be:
?- consult(data).where data is the name of the file to read from. The argument could also be an instantiated variable. Sometimes files will have names that do not meet the requirements of a PROLOG constant, for instance, there is the file with the name, data.23. Consulting this file requires placing the file name in single quotes:
?- consult('data.23').
There is another notation for consulting one or more files in a
single command. It looks just like a list of constants:
?- [data,'data.23','data.24'].To see all the facts and rules PROLOG has use the listing command:
?- listing.If this produces too much information to be convenient, the facts and rules for some particular predicate, such as ``likes" can be listed using:
?- listing(likes).
Also, we have made mention of the anonymous variable, _, that can be used for pattern matching but which never gets set to any value. This variable can be useful in circumstances when you have to match patterns that contain more details than you really need to know about. For instance, suppose you had some data about Cubs games in the following format:
game(1,april,7,cubs,4,mets,1). game(2,april,8,cubs,1,mets,4). game(3,april,9,cubs,7,cardinals,9). game(4,april,10,cubs,4,cardinals,3). game(5,april,11,cubs,1,astros,8).In this predicate game, the first item is the game number, the second item is the month in which the game was played, the third item is the day of the month, the fourth item gives one team name (always the cubs), the fifth item is the number of runs the Cubs scored, the sixth item is the name of the other team involved in the game and the seventh item is the number of runs this other team scored. Suppose your problem is to count up the number of games the Cubs won. In this case, you only need to instantiate variables to the the two scores. You can write:
game(_,_,_,_,Cubruns,_,Opponentruns)This saves you from having to think up names for unused variables and it informs a reader of the program that the fields with an underscore are not relevant to the problem.
In section 4.2 we mentioned that there are procedures, assert and retract to add and subtract entries from the database. Assert actually puts the new clause at the end of the database. In addition, assertz does the same thing, and there is also an asserta that places clauses at the beginning of the database.
In section 4.2 we said that there are not any naturally occurring global variables in PROLOG, however now we will go and demonstrate two ways of simulating global variables. To illustrate the methods we will use a small PROLOG program that counts how many games the Cubs won using data like that shown above. The first method involves using assert and retract. The basic plan we use here will be to simulate a loop that selects a game and checks to see if the Cubs won. Initially, we have to set the number of games the Cubs won to 0. This is easily done like so:
assert(havewon(0)).Later as the program runs thru the list of games, this statement will have to be updated every time it finds the Cubs won a game. The rules for the entire problem are:
count :- assert(havewon(0)),
count2.
count2 :- game(_,_,_,_,Cubruns,_,Opponentruns),
Cubruns > Opponentruns,
retract(havewon(Totalsofar)),
Newtotal is Totalsofar + 1,
assert(havewon(Newtotal)),
fail.
count2 :- write('The Cubs won '),
havewon(Totalwon),
retract(havewon(Totalwon)),
write(Totalwon),
write(' games.'),
nl.
To get the number of games the Cubs won, call count. Count asserts that
the number of games won is 0 and then count2 is called where games are
selected and the scores are checked. In count2 select a game, then
check if the Cubs won and if so then the havewon count needs to be
updated. To do this, retract is used to remove the havewon entry and at
the same time Totalsofar is instantiated to the number of games won.
One is now added to this number and placed in the variable, Newtotal.
Now we assert, havewon(Newtotal). The final test in the rule, is fail,
a built-in predicate that always fails and this forces the interpreter
to back up and look for alternatives. The first step PROLOG finds where
an alternate solution is possible is the step that looks for another
game so the next game is found and the process is repeated over and over
until no more games can be found. When it runs out of games to try, the
interpreter moves on to the second definition of count2 where it simply
prints the answer. The number of games the Cubs have won is then
retracted to keep it from possibly getting in the way of other
questions.
The second method of simulating global variables is to use the record predicates, recorda, recordz and recorded, however, not all PROLOGs have these predicates. With these predicates the system has access to a second database of facts that is structured slightly differently. The basic arguments to recorda (or recordz or recorded) are:
recorda(Key,Term,Reference)Key is just some kind of indexing feature for the Term that is stored away and Reference is a system generated identifying code. For the problem we are working on, we could choose the Key to be, ``havewon" and Term to be ``0". A call to recorda with these parameters together with the PROLOG output is shown below:
?- recorda(havewon,0,R). R = $record(802636)To retrieve the stored information, the recorded predicate is used like so:
?- recorded(havewon,X,R).giving:
X = 0, R = $record(802636)While recorda places entries at the top of the internal database, recordz places them at the end of the internal database. In addition, to erase a record, the erase predicate is called with the proper reference value:
?- recorded(havewon,0,R), erase(R).It should be pretty clear that to find out the number of games that the Cubs won, the previous PROLOG program can just be adapted to use recorda, recorded and erase instead of assert and retract:
count :- recorda(havewon,0,R),
count2.
count2 :- game(_,_,_,_,Cubruns,_,Opponentruns),
Cubruns > Opponentruns,
recorded(havewon,Totalsofar,R1),
erase(R1),
Newtotal is Totalsofar + 1,
recorda(havewon,Newtotal,R2),
fail.
count2 :- write('The Cubs won '),
recorded(havewon,Totalwon,R),
erase(R),
write(Totalwon),
write(' games.'),
nl.
From time to time, either method of simulating global variables can be useful but in general the iterative approach shown here for finding solutions is awkward to impossible on larger problems and PROLOG programmers need to get used to using recursive programming methods.
PROLOG has a data structuring facility that uses functors , to create structures . Structures are much like records in Pascal. A predicate with arguments is in fact a structure that the interpreter will evaluate to true or false. For an example of structure use, here are some definitions that give the contents of some compact disks, where ``cd", ``conductor", ``orchestra", ``contains", ``composer" and ``title" are all functors:
cd(1,conductor(mehta), orchestra('los angeles'),
contains(composer(strauss, richard),
title('alpine symphony'))).
cd(2,conductor(slatkin), orchestra('st louis'),
contains(composer(copland), title('billy the kid')))
cd(3,conductor(abbado), orchestra(chicago),
contains(composer(tchaikovsky), title('symphony no 5'))).
Now to look up pieces of music in the database by Richard Strauss, we
can ask PROLOG:
?- cd(_,_,contains(composer(strauss,richard),title(X))).Note that in this case if we just tried to look up the composer, as strauss with only one field, it would fail because the number of arguments for the functor, composer, would not match:
?- cd(_,_,contains(composer(strauss),title(X))).For another example, suppose we know the title of a work and we want to know who the composer is. We could ask PROLOG:
?- cd(_,_,_,contains(X,title('alpine symphony'))).
Then PROLOG will report, X = composer(strauss,richard).
Internally, structures like ``contains" are trees as shown in figure
12.1.

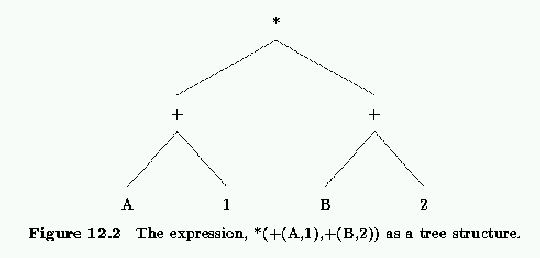
In section 4.2 we said that arithmetic expressions are actually stored internally in a structure format. The infix expression:
(A + 1) * (B + 2)becomes internally:
*(+(A,1),+(B,2))Naturally, this is also a tree structure as shown in figure 12.2.
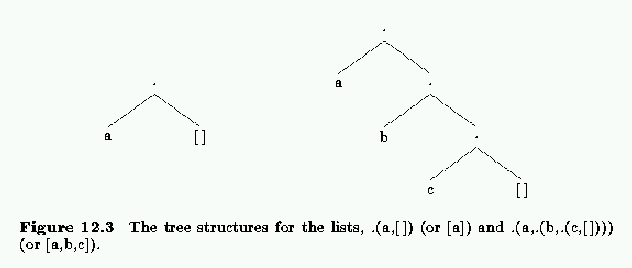
Lists are also defined using the functor, ``." pronounced ``dot". For a list containing just the symbol a, it is written out as:
.(a,[]),where [] corresponds to a special constant called the empty list. The above structure corresponds to the tree on the left in figure 12.3. The list containing the symbols a, b and c is:
.(a,.(b,.(c,[]))),and its tree structure is shown on the right in figure 12.3.
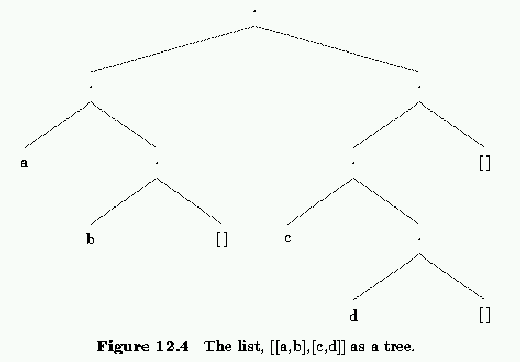
[a,b,c]Lists within lists are allowed and one such list, together with its tree structure is shown in figure 12.4. Recall that the ``|" operator can be used to split a list into a head and a tail. Actually if you look at the tree that represents the list, the head of the list represents the expression below and to the left of a dot while the expression below and to the right represents the tail of the list.
PROLOG also has a set of relational operators available for
comparing numbers and terms. These are the straightforward ones:
|
?- X = 5. ?- X = Y. ?- X + Y = a + b.In the first case, X will be instantiated to 5, in the second case, X and Y will share and in the third case, X will be instantiated to a and Y will be instantiated to b. The following ``comparisons" produce no:
?- 4 = 5. ?- 5 + 3 = a + 3.Some PROLOGs have the relational inequality operator, \=, that succeeds when = fails. The operator, == tests to see if two terms are equal without trying to match both sides. Below are some comparisons and their results:
?- X == 5. no ?- a(b,c) == a(b,c). yes ?- a(B,C) == a(b,c). no ?- X == Y. no ?- X = Y, X == Y. yesIn the last case, X and Y are first made equal, so naturally, X == Y succeeds. The opposite of == is \==. Here are some comparisons and their results:
?- X \== 5. yes ?- a(b,c) \== a(b,c). no ?- a(B,C) \== a(b,c). yes ?- X \== Y. yes ?- X = Y, X \== Y. noTo invert results, C-PROLOG has a not predicate and C-PROLOG and UNH PROLOG both have a not operator, \\+ that inverts results. These questions then, all come out, no:
?- not(X = 5). ?- \+ X = 5. ?- not(X = Y). ?- \+ X = Y. ?- not(X + Y = a + b). ?- \+ (X + Y = a + b).while the following all come out yes:
?- not(4 = 5). ?- \\+ 4 = 5. ?- not(5 + 3 = a + 3). ?- \\+ (5 + 3 = a + 3).PROLOG also provides two other operators for doing numerical comparisons that don't attempt to make the two sides match. The operator, =:= compares numeric values looking for equality and the operator, =\= compares numeric values looking for inequality. The following tests succeed:
?- 1 =:= 1. ?- 1 =\= 2.while these tests fail:
?- X =:= 5. ?- X =\= 5.
The usual built-in arithmetic operators are +, -, *, /, mod and some implementations may have the integer division operator, div. Many PROLOGs also have predicates available to evaluate trigonometric and exponential functions. Some PROLOGs give users the ability to define new operators.
There is an important pseudo-goal in PROLOG, called the cut that is represented by an exclamation point (!). The cut is designed to prevent back-tracking by the PROLOG interpreter. It has a couple of practical uses and it can sometimes be used to increase the efficiency of PROLOG programs. A very simple use of the cut can be seen in the following PROLOG rule:
g :- a, b, c, !, d, e, f.When PROLOG comes across this rule it of course tries to prove each goal in order. However, if PROLOG should happen to prove c, the pseudo-goal, !, automatically succeeds but it also forms a barrier that prevents backtracking to the left of the cut. PROLOG can roam about the right side of the cut, back-tracking as necessary, but if all the alternatives there fail and PROLOG tries to backtrack to the left of the cut, the whole process fails. Here is a short program using this rule:
a :- assert(d).
b :- assert(e).
b :- assert(f(1)).
c.
g(X) :- a, b, c, !, d, e, f(X).
g(X) :- print('will not reach here with a cut'), nl.
If we ask PROLOG to evaluate g(Y), PROLOG will report, ``no". It starts
by looking at the first g(X) rule. It calls a, which asserts d is true.
It calls b which asserts e is true. It finds c is true and then passes
the cut. It then finds d and e are true but it will not find f(X) is
true. Without the cut, PROLOG would back up and try the second
definition of b and that second definition would assert what is
necessary for f(X) to succeed. With the cut present, the first g(X)
rule simply fails and you would expect that PROLOG would simply go on to
the second g(X) rule and succeed but in fact it does not go on to the
second rule. When the first rule for g(X) failed, the existence of the
cut in the first rule caused all other rules with the g predicate to
also fail, so the second g rule isn't even tried.
This feature of the cut that causes all rules with the same predicate at the head of the rule to fail can be put to good use. Here it is used in a definition of factorial:
/* 1 */ factorial(N,M) :- N < 0, !, fail.
/* 2 */ factorial(0,1).
/* 3 */ factorial(N,M) :- X is N-1,
factorial(X,Y),
M is N * Y.
Rule number 1 is designed to trap any request for the factorial of
a negative number. If the user tries this, PROLOG will not attempt
to find another way to satisfy the factorial predicate. In addition,
someone might ask PROLOG for the factorial of a legitimate number,
like, 3. After PROLOG responds with the answer, 6, a mischievous user
could go ahead and type a ; that would set PROLOG off on an effort to
find a second solution that just simply doesn't exist. Again, the cut
in statement 1 prevents this.
In this section we will look at ways to do input and output of terms and characters as well as at some related predicates.
A term is either a number, a constant or a structure built up out of a functor with arguments. There is a built-in predicate, read, to read terms. It requires that the term be followed by a period. If the call to read is: read(X), then terms such as the following can be read:
99. 97.1. hello. 'Fort Laramie'. likes(john,mary). likes(X,yankees) :- likes(X,lemonade).This last term really isn't any problem because PROLOG regards the :- symbol as just another operator and the rule as just another structure. The default is to do reads from the terminal input file. It is possible to read from another file by using the predicate, see, as in the following example where terms will be read from the file, f:
?- see(f), read(X), read(Y), read(Z),
print(X), tab(4),
print(Y), tab(4),
print(Z), nl,
seen.
In the above example, the first three terms on the file, f, will be
read. The first term read will be printed, then 4 blanks will be
printed, then the second term will be printed, then four blanks, then
the third term and then the end of line. Notice that tab(N) writes out
N blanks and does not move to column N, as might be expected.
The function of the seen predicate is to reestablish the terminal input
file as the default file to read from. If you try to read beyond the
last term on the file, the variable will first come back with the value,
end_of_file and if another read beyond this is attempted the request
being processed will fail.
When it comes to printing terms, the predicates write and print are identical and they each output a single term. If a term contains operators, then write and print both write out the term by transforming its internal structured representation to infix notation. For instance, write(+(a,b)) produces:
a + bTo force terms to be printed as they are in their internal structured representation, the predicate, display can be used, thus, display(+(a,b)) produces:
+(a,b)When it comes to backtracking across the predicates, read, write, print, tab, display and nl, PROLOG will not try to re-satisfy them. For instance, it might occur to you to try to read and write all the terms in a file using the following scheme:
?- see(f), read(X), print(X), X = end_of_file, seen.The first item in the file will be read and printed. If this first item is not the end of file constant, PROLOG will start backtracking but it will not try to do another read. To read and write every term in a file a recursive solution is necessary.
Ordinarily, write, print, tab, display and nl apply to the standard terminal output file. To switch to another file, the predicate, tell, is called. Its argument should be instantiated to the name of the file to print on. To end output to the file and return to writing to the standard terminal file, the predicate, told, is called. An example of this where output goes to the file, f, would be:
?- tell(f), print('Hello World'), nl, told.
PROLOG also has predicates for reading and writing individual characters. The predicate, put, will write out a single character. Unfortunately, the argument has to be the integer representing the ASCII character, so, to print ``hello" using put you have to say:
?- put(104), put(101), put(108), put(108), put(111).Of course this is rather inconvenient, if it is just a matter of printing hello, it is better to use print or write:
?- print(hello).Another feature of PROLOG is that it will consider a string of characters enclosed in double quotes to be a list of integers representing the characters. Therefore, if we enclose hello in double quotes it is the same as the list:
[104, 101, 108, 108, 111].With a list of characters it is easy to devise a recursive procedure to print them all out:
putstring([]) :- !. putstring([A | Rest]) :- put(A), putstring(Rest).Using this scheme we could get PROLOG to print out hello, just by typing:
putstring("hello").
Of course, this approach isn't all that convenient compared to just
using print to output the equivalent constant.
Characters are read using get and get0. When called with an uninstantiated variable, get will instantiate that variable to the next printing character in the input stream. Printing characters are those that will show up on the terminal screen so control characters will be skipped over. Get0, on the other hand, will return the very next character no matter what it is. Unfortunately, there is no way to look ahead to see the next character without reading it, as is the case in Pascal with its file buffer variable. Neither is there a predicate that will ``un-get" a character as in C. PROLOG programmers, can however, create their own predicates to do these things.
To illustrate character reading plus some other useful PROLOG predicates, we will work on building a very small interpreter that will take three word sentences from the keyboard. The sentences will be either a statement of fact, ending in a period, or a question, ending in a question mark. Some examples of the type of input the program will take are the following:
john loves mary. mary loves fred. john loves baseball. john loves mary? mary loves baseball?For a statement of fact, the fact will be be added to the database. For a question, the question will be passed on to the PROLOG interpreter to determine whether it is true or not.
To start with, we need a predicate that will scan the input looking for the first character that is not a blank. The following two statements define, scan, a predicate that will do this:
/* 1 */ scan(C,C) :- C =\\= 32, !. /* 2 */ scan(C,C2) :- get0(C1), scan(C1,C2).To use scan we have to supply it with a character (first argument), which it checks to see if it is a blank (ASCII 32) or not. If it is not a blank then it returns the character (second argument) otherwise scan will read a character using get0 and pass that character on to another call of scan. The process continues until a non-blank is found. To get the process started, scan will of course have to be supplied with an initial character as in:
?- get0(X), scan(X,Y).
Now that we have the procedure scan that can find the first letter of a word, we will work on accumulating all the characters in the word in a list. Every word will be terminated by either a blank, a period or a question mark. When we find a blank we will do nothing special. When we find a period or a question mark, we will need to assert that end_of_sentence is true and in addition, for a question mark, we will assert that question is true. Here are the PROLOG rules to accomplish this:
/* 3 */ rw(W) :- get0(X), scan(X,A), rest(A,W).
/* 4 */ rest(32,[]).
/* 5 */ rest(46,[]) :- assert(end_of_sentence).
/* 6 */ rest(63,[]) :- assert(end_of_sentence),
assert(question).
/* 7 */ rest(C, [C | R]) :- get0(X), rest(X,R).
The basic predicate to call is rw, for read word. The call, rw(X) will
produce a prompt for input. If we type in: ``hello.", then PROLOG
reports:
X = [104, 101, 108, 108, 111].The way rw works is quite straightforward. First, get a character to start the problem and call scan to possibly read characters until a non-blank is found. When this first letter, A, has been found, it is passed on to the predicate, rest. Rest will accumulate the rest of the letters in the word and return W, the complete list of characters in the word, W. Rest is also straightforward. Its first argument is the character to examine. Rules 4, 5 and 6 check for an end of word indication, either a blank (32), a period (46) or question mark (63). All three of these rules return [ ] to finish off the list of characters and these rules also stop the recursion. If the character is not any of these word ending characters then go on to rule 7, where another character is read, added to the list and rest is called again.
The next problem is to read a whole sentence. In our particular case, we could resort to just reading three words, but for the sake of generality, we will assume that there can be an arbitrary number of words in each sentence. The predicate to do this is rs, for read sentence. The solution follows the typical recursive pattern. Rs reads one word, then calls up rs again to read the rest of the words, and so on until rs finds it can retract the end_of_sentence fact that was asserted by rest. The rules are:
/* 8 */ rs([]) :- retract(end_of_sentence). /* 9 */ rs([W|R]) :- rw(W), rs(R).Rs is called with a single argument, as in:
?- rs(S).If the user types in:
john loves mary.rs produces:
S = [[106,111,104,110],[108,111,118,101,115],[109,97,114,121]]With the sentence in this form we will go ahead and convert each list of characters to a single atom. The built-in PROLOG predicate, name, does this. As an example of how name works we will take the list of characters for john and convert it to an atom like so:
?- name(X,[106,111,104,110]). X = johnIt is also possible to take an atom and convert it into a list of integers as in:
?- name(hello,X). X = [104,101,108,108,111]With this capability, it is easy to convert a list of lists of characters into a list of atoms. The predicate to do this will be called mkatoms. Its first argument will be the list of lists of characters and its second argument will be the list of atoms:
/* 10 */ mkatoms([],[]).
/* 11 */ mkatoms([A|B], [Namea|Namerest]) :- name(Namea,A),
mkatoms(B,Namerest).
In this example, we use rs and mkatoms and type in, ``john loves mary.":
?- rs(S), mkatoms(S,L).giving:
S = [[106,111,104,110],[108,111,118,101,115],[109,97,114,121]], L = [john,loves,mary]
The next step in turning a list, like L, above, into a fact that can be asserted is to reverse the first two items in the list. Reversing the first two items can be done like so:
?- Y = [john,loves,mary], Y = [A,B,C], Z = [B,A,C].The first clause merely sets a value for Y, then Y is then matched against the pattern, [A,B,C], giving:
A = john, B = loves, C = maryand finally, Z is set equal to the list, [B,A,C], giving:
Z = [loves,john,mary]From here we can use the built-in operator that consists of an equal sign followed by two dots, =.. and pronounced ``univ" to produce an ordinary PROLOG term. An example of the use of =.. is:
?- P =.. [loves,john,mary].which gives:
P = loves(john,mary).Of course, =.. will happily take a PROLOG term and turn it into a list of atoms, as in:
?- likes(matt,mets) =.. L.giving:
L = [likes,matt,mets]Now we can read a sentence, rearrange the words and convert it to a term. The predicate, interpret, shown below does this:
/* 12 */ interpret :- rs(X),
mkatoms(X,Y),
Y = [A,B,C],
Z =..\ [B,A,C],
interpret2(Z).
Notice that interpret passes the term, Z, on to interpret2. The clauses
for interpret2 will examine the data base and see if the sentence is a
question to be answered or a fact to be added to the data base. The
definition for interpret2 is:
/* 13 */ interpret2(Z) :- question,
call(Z),
retract(question),
print('absolutely!'),
nl.
/* 14 */ interpret2(Z) :- retract(question),
print('no way!'),
nl.
/* 15 */ interpret2(Z) :- assert(Z),
print('ok!'),
nl.
In rule 13, PROLOG checks to see if question is true. If it is, the
call predicate will pass the term, Z, on to the PROLOG interpreter. If
this call succeeds the rest of rule 13 will retract question and print
out the response 'absolutely!'. In this case, that will be the end of
the call to interpret as well. The call predicate may fail, however, in
this case PROLOG will back-track from the call and be forced to go on
to rule 14. Rule 14 will try to retract question and if it can, this
means that the call in 13 failed and so rule 14 prints out 'no way!'.
On the other hand, if 14 fails, Z must have been a statement of fact and
PROLOG will move on to rule 15 and enter the fact into the data base.
This whole arrangement requires the user to type in, ``interpret.", every time a fact is entered or a question is asked. Of course it would be easy to devise a predicate to repeatedly call interpret until some special sentence like, ``halt." is entered. Figure 12.5 lists the whole program.

In this section we will look at a few extra examples of PROLOG programs involving the manipulation of lists.
The first example to look at will be a tree search procedure with the predicate named, ts. The first argument is the tree to search and the second argument is the item to search for. Its definition looks just like the recursive versions that can be programmed in conventional languages:
/* ts1 */ ts([],Item) :- fail. /* ts2 */ ts(Tree,Item) :- Tree == Item. /* ts3 */ ts([First|Rest],Item) :- ts(First,Item). /* ts4 */ ts([First|Rest],Item) :- ts(Rest,Item).A sample call to ts would be:
ts([*, [+,a,b], [+,c,d]], [+,a,b]).As to how ts works, rule ts1 says that the item can't be found in an empty list, so return failure. Rule ts2 tests to see if the tree it has been given is the entire item. Rule ts3 looks for the item within the first part of the tree and rule ts4 looks for the item within the rest of the tree.
When an item is found within a tree it is often necessary to substitute another expression for it. For example we may want to go through a tree and substitute 3 for every occurrence of x. In the subst predicate defined below the first parameter gives the tree to search and the second item is the expression to be replaced. The third item is the replacement for the second expression and the fourth argument is a new tree in which the replacements have been done. Here is the definition of subst:
/* s1 */ subst([],Old,New,[]).
/* s2 */ subst(Tree,Old,New,New) :- Tree == Old.
/* s3 */ subst(Tree,Old,New,Tree) :- atomic(Tree).
/* s4 */ subst([First|Rest],Old,New,[Newfirst|Newrest]) :-
subst(First,Old,New,Newfirst),
subst(Rest,Old,New,Newrest).
Rule s1 states that if the tree to search is empty, the resulting
tree is also empty. Rule s2 tests to see if the whole tree is equal
to the pattern we want to replace and if it is, the resulting tree is
the new expression. Rule s3 catches a tree that consists of a single
atom and sends back that atom. The predicate, atomic, in that rule
tests for single atoms. If none of these rules succeeds, then we apply
subst to the first part of the tree to produce a new first part and then
apply subst to the rest of the tree to produce a new rest of the tree.
The answer to send back is a new tree with the new first part on the
left and a new rest part on the right.
One of the most important list manipulation predicates a PROLOG programmer needs is the append predicate that appends, or concatenates two lists together. It has other interesting capabilities as well. The definition of append is quite short:
append([],L,L). append([A|L1],L2,[A|L3]) :- append(L1,L2,L3).This definition of append means that if you concatenate together the first argument with the second argument you produce the third argument. For example:
?- append([a,b,c],[1,2,3],L).gives:
L = [a,b,c,1,2,3]The method of operation follows the usual pattern of recursive definitions. The second of the two rules is designed to split off from the first argument one item for each recursive call until it becomes the empty list. In the above example, in the first call, a will be split off and it will go on the front of the third argument. The rest of the third argument is undefined at this point. To define it, the append predicate is called again, minus the a on the front of the first argument. This call will put b on the front of the third argument and the third call will put c on the front of the third argument. Finally, when the first argument becomes the empty list, the first rule applies and the result becomes the second argument. At this point, the third argument in the first call of append (when a was broken off) is completely instantiated.
Append can be used to do more than run lists together. First, we can give a value for the first and third argument and PROLOG will find the value of the second argument as in this example where:
?- append([a,b,c],L,[a,b,c,1,2,3]).gives:
L = [1,2,3]Second, if we give the second and third argument, PROLOG will find a value for the first argument:
?- append(L,[1,2,3],[a,b,c,1,2,3]).gives:
L = [a,b,c]Finally, if only the third argument is instantiated, PROLOG can go and find all the different ways that the first and second arguments can be instantiated to produce the third:
?- append(X,Y,[a,b,c,1,2,3]).
X = [], Y = [a,b,c,1,2,3];
X = [a], Y = [b,c,1,2,3];
X = [a,b], Y = [c,1,2,3];
X = [a,b,c], Y = [1,2,3];
X = [a,b,c,1], Y = [2,3];
X = [a,b,c,1,2], Y = [3];
X = [a,b,c,1,2,3], Y = [];
We will look at how this last task is accomplished since it is a little messier than other PROLOG problems we have tried. PROLOG starts by matching against the first rule giving this solution:
append([],[a,b,c,1,2,3],[a,b,c,1,2,3]).When we ask for more by typing a semi-colon, PROLOG moves on to the second rule where PROLOG notices that X can match the list, [A|L1], Y can match the list, L2 and [a,b,c,1,2,3] matches [A|L3] with A then becoming, a, and L3 then becoming [b,c,1,2,3]. We can make the matches more apparent by writing the two terms one above the other like so:
append( X, Y, [a , b,c,1,2,3]). append([A | L1],L2, [A | b,c,1,2,2]).If the tail of rule 2 can be made to succeed, a new solution will be found. The tail becomes the problem:
(1) append(L1,L2,[b,c,1,2,3]).This matches with rule 1 giving L1 = [ ], L2 = [b,c,1,2,3]. PROLOG can now give the solution:
append([a],[b,c,1,2,3],[b,c,1,2,3]).If the user asks for another one, PROLOG will be using the call above labeled (1). Asking PROLOG for more can be regarded as a user created failure of rule 1, so PROLOG moves on to rule 2. PROLOG finds it can match (1) like so:
(1) append( L1, L2, [b | c,1,2,3]). (2) append([A | L1], L2, [A | c,1,2,3]).Here in the line labeled (2), remember that the L1 and L2 are entirely new variables in another call and are not the same as the L1 and L2 in the line labeled (1). Since the heads can be made to match, PROLOG goes off on the new problem:
append(L1,L2,[c,1,2,3]).Of course, this matches the first rule and PROLOG can report the next solution:
append([a,b],[c,1,2,3],[a,b,c,1,2,3]).This whole cycle can continue until it becomes impossible to break off another item in rule 2. This kind of scheme whereby a PROLOG predicate can have different combinations of its variables instantiated and still find solutions for the other uninstantiated variables has been referred to as ``reversible programming".
Sorting is a major preoccupation of Computer Science and so it is interesting to see some sorting algorithms done in PROLOG. These algorithms can be remarkably compact. The first one we want to look at will be quicksort. We will work on this problem from the top down. The first step is to state that the quicksorted version of the empty list is the empty list:
/* qs1 */ qs([],[]).
If the list to be sorted is not empty, then we will take the first number in the list, call it K, and use it to partition the rest of the list into a left part where all the numbers are less than K and a right part where all the numbers are greater than or equal to K. We simply sort these two pieces and put together a new list with the sorted left portion followed by K, followed by the sorted right portion. To put the pieces together we can use append. The rule to do all this is quite straightforward:
/* qs2 */ qs([K|Rest],Sorted) :-
partition(K,Rest,Left,Right),
qs(Left,Sortedleft),
qs(Right,Sortedright),
append(Sortedleft,[K|Sortedright],Sorted).
For example, if we want to quicksort the list, [19, 5, 23, 17, 89, 0,
101], partitioning will produce:
|
|
|
We are now left with the problem of defining the partition predicate. As usual, we will break off the first number from the list and deal with it. If it is less than K it will be put on the front of the Left list by this rule:
/* qs3 */ partition(K,[A|Rest],[A|Left],Right) :-
A < K,
partition(K,Rest,Left,Right).
otherwise, the following rule will put it on the right side:
/* qs4 */ partition(K,[A|Rest],Left,[A|Right]) :-
A >= K,
partition(K,Rest,Left,Right).
Actually, if the rules labeled qs3 and qs4 are in order, the
test, ``A > = K" isn't even needed. Again, as usual, when there are
no more elements to break off the list, we stop the recursion this time
using:
/* qs5 */ partition(K,[],[],[]).
The second sort we will look at will be the selection sort. Recall that the principles of selection sorting are that the list is searched to find the largest (or smallest) number in the list, the number is removed from the original list and then this number is placed at the beginning (or the end) of another list. In this version, we will work on finding the largest number and place it at the beginning of the sorted list, giving a list in descending order of values. Again, sorting an empty list is quite easy:
/* ss1 */ ss([],[]).but sorting larger lists requires more effort. To do this we take the whole list and split it into a tentative maximum value, Tmax and R, the rest of the list. We find the maximum value, Max, in the whole list, [Tmax|R] and call the list without Max, L. We perform the sorting of L and the result will be the list, Sorted. The final answer for the completely sorted original list will be Max followed by Sorted. In PROLOG, this is:
/* ss2 */ ss([Tmax|R],[Max|Sorted]) :-
max([Tmax|R],Tmax,Max,L),
ss(L,Sorted).
The remaining problem is to find the largest number in the list
and remove it. Finding the largest number is straightforward. The
solution is to break one number at a time off the list and work
with it. If it is larger than Tmax, then send off this new larger
value to the next call, otherwise simply pass on the current largest
value. Rule ss4, below, sends down a new larger number and rule ss5
sends down the current largest value. Rule ss3 catches the case
where there aren't any more values to test. In this case, the
actual maximum value becomes the tentative maximum value. Here is
the definition of the max predicate:
/* ss3 */ max([],Max,Max,[]).
/* ss4 */ max([A|R],Tmax,Max,Back) :- A > Tmax,
max(R,A,Max,B),
remake(A,Max,B,Back).
/* ss5 */ max([A|R],Tmax,Max,Back) :- max(R,Tmax,Max,B),
remake(A,Max,B,Back).
As outlined above, max finds the largest value on the way ``down",
now, on the way ``up", max constructs a new list that does not contain
the largest value. Rule ss3 supplies the initial list, the empty list,
to send back up. Suppose on return from ss3, PROLOG finds itself in
rule ss4 with B equal to the empty list. The predicate, remake is
called to compare the selected number, A, in this call with Max to see
if it should be added to the list that will be sent back. The current
list is supplied to the predicate remake as the third argument. If
A = Max then rule ss6 (below) sends out in the fourth argument the same
list as the list going in otherwise rule ss7 sends back the number added
onto the list:
/* ss6 */ remake(A,Max,Back,Back) :- A =:= Max. /* ss7 */ remake(A,Max,Back,[A|Back]).Notice that this arrangement will not be able to correctly handle lists with duplicate entries. So the call:
?- ss([1,1,2,3],X), produces: X = [3,2,1].We leave it as an exercise to modify the program to handle duplicate values.
| 12.1. |
[a,b,[c,d]] [[a,b,[c,d]]] [[a,[b,c],d]] [[a,b,[c,d],[e,f],[g]]]
| 12.2. |
a :- assert(d).
b :- assert(e).
b :- assert(f(1)).
c.
i.
i :- assert(f(2)).
j.
g(X) :- a, b, c, !, d, e, f(X).
g(X) :- print('will not reach here with a cut'), nl.
h(X) :- i, g(X), j.
| 12.3. |
| 12.4. |
a)Write a PROLOG program that will search a binary search tree for a given number. Naturally you will take advantage of the order within the tree to do the search quickly.
b)Write a PROLOG program to insert numbers into a binary search tree. You may want to store the tree in the database and retrieve it when necessary.
c)Write a PROLOG program to delete a number from a binary search tree.
| 12.5. |
bubsort(U,S) :- append(X,[A,B|Y],U),
A > B,
append(X,[B,A|Y],N),
bubsort(N,S).
bubsort(L,L).
Explain how this PROLOG program works. Suppose when PROLOG returns a
sorted list the user types a ``;" to make PROLOG look for an alternate
answer. What happens?
| 12.6. |
| 12.7. |
| 12.8. |
?- +(a,b) =.. L. L = [+, a, b]However, univ will only convert the top level structure to a list. It will convert *(3,exp(x)) to [*,3,exp(x)] and not to [*,3,[exp,x]]. Write a PROLOG function that will take a structured expression and turn it into a list that does not contain any structures, but only more lists that represent embedded structures. For instance, suppose we name the function to do this problem, us, for unstructure, then:
|
|
| 12.9. |
deriv(X,X,1) :- atomic(X).where atomic is a predicate that tests for an atom. Another example would be that the derivative of the sum of two functions is the sum of the derivatives of the functions:
deriv([+,U,V],X,[+,DU,DV]) :- deriv(U,X,DU), deriv(V,X,DU).In the above example we represented complex expressions in a list notation with the function at the start of the list. If U and V are arbitrary functions and C is an integer constant, write PROLOG rules to find the derivatives of at least the following functions:
|
| 12.10. |
game(1,april,7,cubs,4,mets,1). game(2,april,8,cubs,1,mets,4). game(3,april,9,cubs,9,cardinals,7). game(4,april,10,cubs,4,cardinals,3). game(5,april,11,cubs,1,astros,8).You might want to generate data for the Cubs or for your favorite team with possibly up to 162 games for a full season. Write PROLOG functions to determine:
a)how many games the Cubs won, b) how many times the Cubs beat a particular team such as the Cardinals, c)how many games did the Cubs win in a particular month, d)what was the Cubs longest winning streak in general and e) what was the Cubs longest winning streak against a particular team. This should take into account that the Cubs may beat one team, say the Mets, then win or lose a number of games against some other team or teams and then win some more games against the Mets.
Of course, there may be other questions you want to program as well. All the above problems should be done recursively and without resorting to the looping-like method described in section 12.1.
| 12.11. |
|
|
| 12.12. |